Küme tanımı ve gösterim yöntemleri
Küme,
adına eleman dediğimiz iyi tanımlanmış ögeleri içeren bir topluluktur. Örneğin alfabenin harfleri, doğal sayılar bir küme oluştururlar. İyi tanımlanmış öge ile kastedilen kümenin elemanlarının belirli olmasıdır. Küme elemanları alfabenin harfleri kümesinde olduğu gibi sonlu olabilir. Ancak doğal sayılar kümesi gibi sonsuz da olabilir. Sonsuz elemanı olsa da doğal sayılar kümesinin elemanları belirlidir. Bir sayının bu kümeye ait olup olmadığını kesin olarak belirleyebiliriz. Dolayısıyla "Sınıfın güzel kızları" bir küme belirtmez. Çünkü güzel kızlar listesi kişiden kişiye değişebilir.
Kümeleri gösterirken üç yolumuz var: Venn şeması, liste yöntemi ve ortak özellik yöntemi:
- Venn Şeması
- Liste Yöntemi
- Ortak Özellik Yöntemi
Çoğunlukla sonlu kümeleri kapalı bir geometrik bölge içine koyarak bir Venn şeması oluşturulur. Her elemanın önüne bir nokta konur.
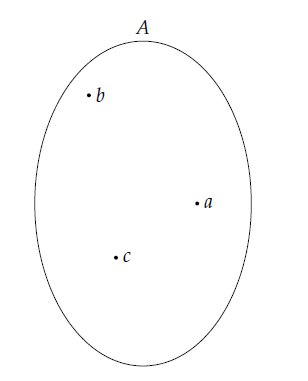 A kümesinin elemanları a,b ve c harfleridir.
A kümesinin elemanları a,b ve c harfleridir.
Kümenin elemanları küme parantezi denilen "{" ve "}" işaretleri arasına virgülle ayrılarak yazılır. Örneğin yukarıdaki A kümesi {a,b,c} şeklinde gösterilebilir. Kümenin elemanları başka kümeler de olabilir örneğin
$ B = \{\{a,b\},a,b,2\} $ kümesinin dört elemanı vardır ve bunlardan biri {a,b} dir. Bir ögenin küme elemanı olduğunu belirtmek için $\in$ ("elemanıdır") sembolü kullanılır. Örneğin $\{a,b\} \in A$ yazabiliriz.
Bu yöntemde küme elemanlarını belirlemeye yarayacak şart veya özellik söylenir. Dolayısıyla aynı küme farklı şekillerde yazılabilir. Örneğin $A = \{ 10$ dan küçük pozitif çift sayılar $\} $ şeklinde tanımlanabileceği gibi $\{ 8$ in pozitif tam bölenleri $ \} $ olarak da tanımlanabilir. Elemanları belirleyen özellik daha sembolik bir yazımla da yapılabilir bu durumda sola elemanı belirten sembol ve sağa da uyulması gereken şartlar yazılır.
\[ A \{ x | x \in \mathbb{N}, 2 \lt x \leq 5 \} \]
Yukarıdaki yazımda $A$ kümesi $x$ elemanlarından oluşmaktadır ve bu elemanlar doğal sayıların elemanı olmalı aynı zamanda da $2 \lt x \leq 5$ eşitsizliğini sağlamalıdır. Dolayısıyla $A$ kümesinin liste gösterimi $\{ 3,4,5 \}$ şeklindedir.
Sonlu ve Sonsuz Kümeler
Eleman sayısı sonlu olan kümelere sonlu küme , sonlu olmayan kümelere de sonsuz küme denir. Sonsuz kümelerden aşağıdaki dört taneyi hatırlarsak:
- Doğal Sayılar Kümesi
- Tam Sayılar Kümesi
- Rasyonel Sayılar Kümesi
- Reel Sayılar Kümesi
\[ \mathbb{N} = \{ 0,1,2,\cdots \} \]
\[ \mathbb{Z} = \{ \cdots,-1, 0,1,\cdots \} \]
$a$ ve $b$ tamsayı ve $b \neq 0$ olmak üzere $\frac{a}{b}$ şeklinde yazılabilen sayılardır.
\[ \mathbb{Q} = \{ \frac{a}{b} | a,b \in \mathbb{Z} , b \neq 0 \} \]
Reel sayılar kümesi rasyonel ve irrasyonel sayılar kümesinin bileşimidir ve $ \mathbb{R} $ ile gösterilir.
Eşitlik, Denklik, Boşküme ve Altküme
$A$ ve $B$ gibi iki kümenin elemanları tamamen birbiri ile aynı ise bu iki kümeye eşittir denir ve $A = B$ şeklinde gösterilir.
$A$ ve $B$ gibi iki kümenin eleman sayıları eşit ise bu iki kümeye denktir denir ve $A \equiv B $ şeklinde gösterilir.
Hiç bir elemanı olmayan kümeye boşküme denir. Boş küme $\emptyset$ sembolü ile gösterilir. Boşküme bir tanedir.
Bir $A$ kümesinin elemanlarının tamamı $B$ kümesinin de elemanı ise $A$ kümesi $B$ nin altkümesidir denir ve $ A \subset B$ şeklinde gösterilir. Boşküme her kümenin altkümesidir. Eşitliğin tanımından çıkarabileceğimiz gibi her küme kendisinin altkümesidir. Bir kümenin kendisi dışındaki altkümelerine özaltkümeleri denir.
Örnek
$A = \{ 1,2,3 \} $ kümesinin altkümelerini yazınız.
Çözüm
Bu kümenin elemanlarını kullanarak oluşturacağımız tüm kümeler bir altkümedir, aynı zamanda boşküme de bu kümenin bir altkümesidir. Tüm kümeleri eleman sayıları ile yazarsak:
- Hiç elemanı olmayanlar: $\emptyset$
- Bir elemanlılar: $ \{1\}, \{2\}, \{3\} $
- İki elemanlılar: $ \{1,2\}, \{1,3\}, \{2,3\} $
- Üç elemanlılar: $ \{1,2,3\} $
Bir kümenin toplam altküme sayısını $n$ eleman sayısı olmak üzere $ 2^n $ formülü ile bulabiliriz. Örneğin yukarıda altkümeleri yazarak $8$ tane olduğunu gördük, $A$ kümesinin eleman sayısı $3$ olduğundan $2^3$ de bize altküme sayısını veriyor.
