Cevap

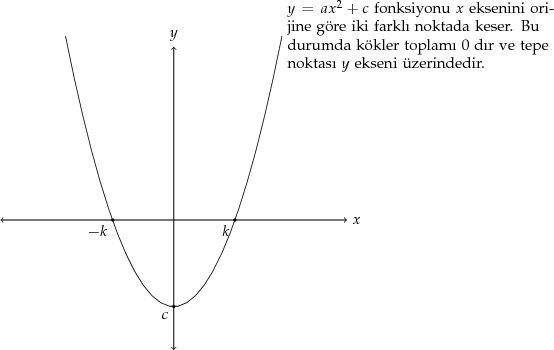
Parabolün $x$ eksenini kestiği yerler denklemin kökleridir. Bunların başlangıç noktasına göre simetrik olması tam ortalarında orijinin olduğunu yani toplamlarının sıfır olduğunu gösterir. Örneğin $-3$ ve $3$ te kesiyordur ve kökler toplamı $0$ dır. Bu durumda $-\frac{b}{a} = 0$ dır ya da $b=0$ dır. Başka bir deyişle kökler toplamı sıfır ise ya da parabolün tepe noktası $y$ ekseni üzerinde ise $b=0$ dır ve denklemde $x$ li terim yoktur. Bu durumda verilen parabol $ y = ax^2 + c$ dir. Bir parabolün alabileceği minimum değer ya da maksimum değerden bahsediliyorsa tepe noktasının ordinatından yani bu noktada alınan değerden bahsediliyordur. Burada tepe noktası $y$ ekseni üzerinde olduğundan $x=0$ dır ve bu noktada alınan değer $y =c$ olur. Demek ki $c = - \frac{1}{7}$ dir. Bulduğumuz $b$ ve $c$ değerlerini sorulan ifadede yerine yazarsak cevap $7$ olur.