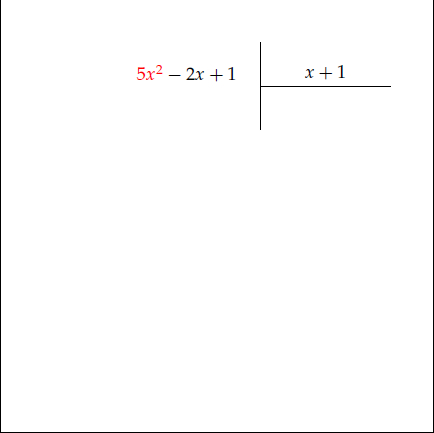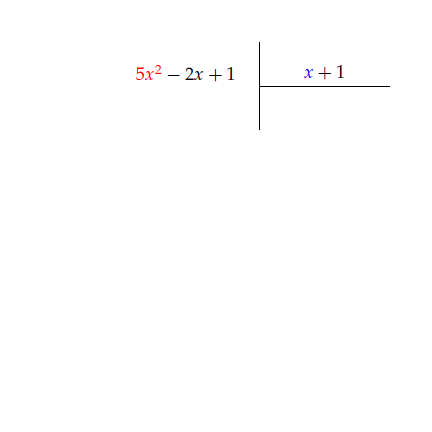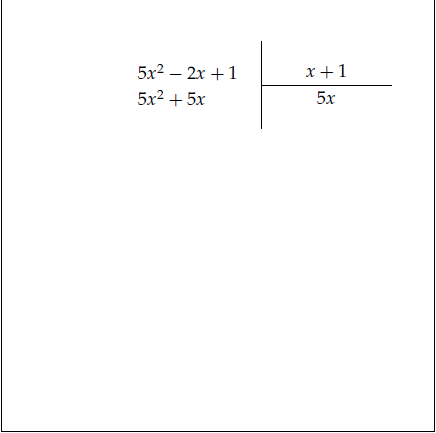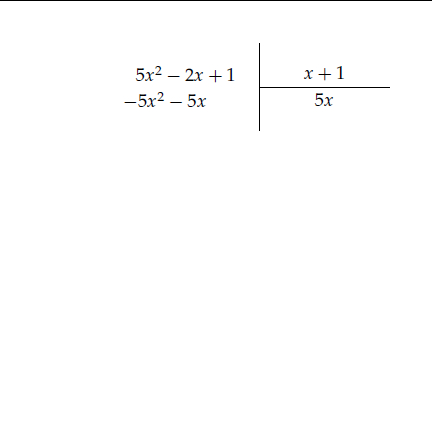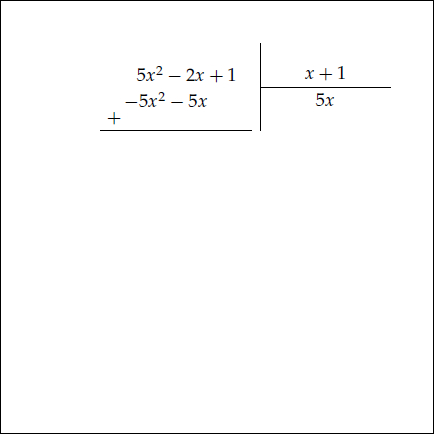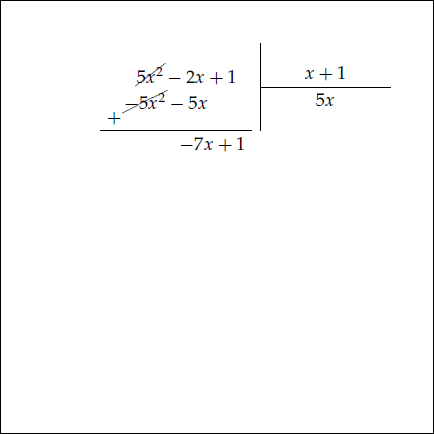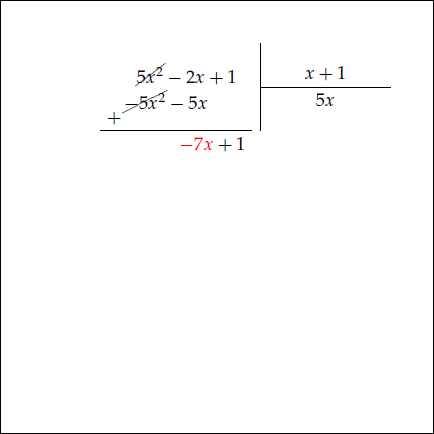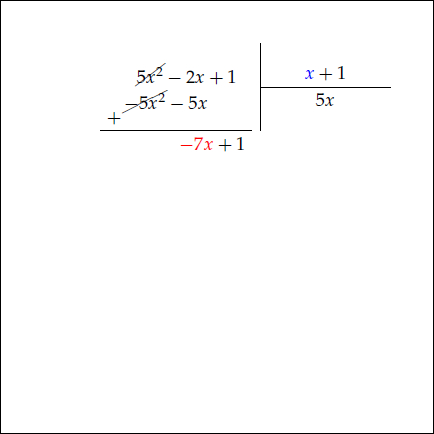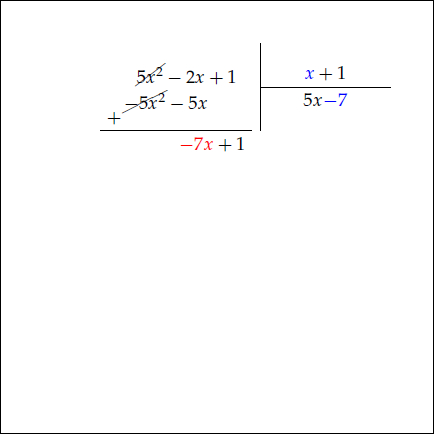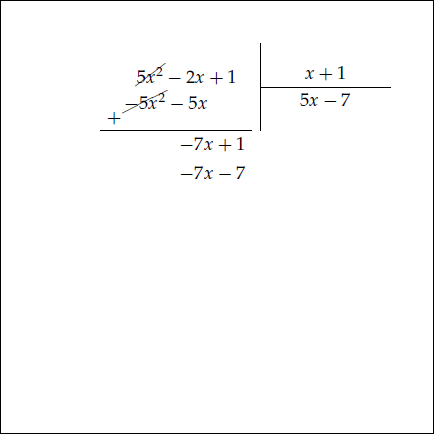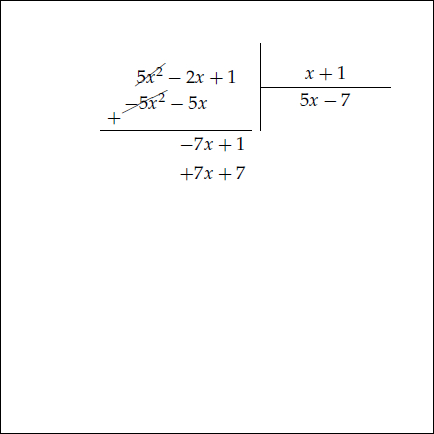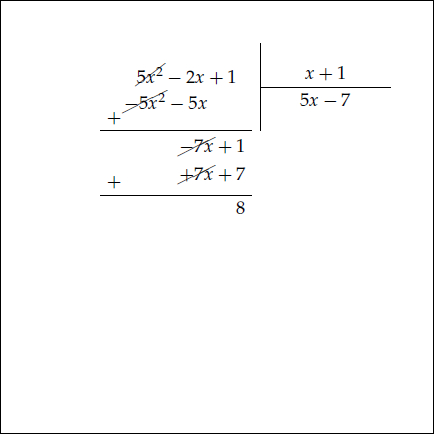ax-b ile bölümünden kalan
Bu bölüm polinomlar konusunun kilit noktasıdır. Hatta polinom konusunun neredeyse tamamı bu bölüm sayılabilir. Bu bölümün örneklerinin tamamen anlaşılması polinom konusu sorularının çözümü için çok önemlidir.
Öncelikle bir polinom diğerine nasıl bölünür bunu gözden geçirelim. Bir $P(x)$ polinomunun başka bir $Q(x)$ polinomuna bölünebilmesi için derecesinin en az $Q(x)$ kadar olması gerekir. Bölme yaparken her adımda en büyük dereceli terimler bölünür ve kalan, bölenin derecesinden az olduğunda durulur.
Örneğin $5x^2 -2x +1$ ifadesini $x+1$ e bölerken önce $5x^2$ terimi $x$ e bölünür. Aşağıdaki animasyonu inceleyiniz.
Bölmenin sonucu bölüm $5x-7$ ve kalan da $8 $ çıkmıştır. Bölmenin tanımı gereği bölünen, bölümle bölenin çarpımına kalan eklenerek bulunabilir.
\[5x^2-2x+1=(5x-7).(x+1) + 8 \]
Yukarıda, ifadenin sağ tarafında şunu görüyoruz. $x+1$ ile böldüğümüzde kalanı bulmak için $x$ yerine $-1$ koymamız yeterlidir. Bu durumda bölen $0$ a eşit olacağından cevap $8$ olur. Demek ki $ax-b$ ye böldüğümüzde kalanı bulmak için bölme yapmadan $x$ yerine $\frac{b}{a}$ konabilir.
Genel konuşursak bir $P(x)$ polinomu $ax-b$ ifadesine bölünürse bölüm başka bir $Q(x)$ polinomudur ve kalan da $k$ gibi bir reel sayıdır.
\[ P(x) = (ax-b)\cdot Q(x) + k \] olduğundan $ax-b=0$ eşitliği çözülür ve bulunan $x$ değeri polinomda yerine konursa kalan elde edilmiş olur.
Örnek
$P(x-1) = 2x^2-3x+3 $ polinomunun $x-1$ ile bölümünden kalan nedir?
Çözüm
$x-1=0 \rightarrow x=1$. Gene burada en çok karıştırılan noktayı vurgulayalım. $P(1)$ falan değil. $x$ yerine $1$ konur hangi polinom bölünüyorsa orda.
\begin{align*}
P(x-1) &= 2x^2-3x+3 \\
P(1-1) &= 2-3+3=2\\
\end{align*}
Kalan $2$ dir.
Polinom soruları genellikle bu kadar basit olmaz. Bize kalanı sorulan polinom hazır verilmeyebilir. Örneğin:
Örnek
$P(x+2)=x^2-x+7$ ise $P(x-1)$ polinomunun $x-1$ ile bölümünden kalan nedir?
Çözüm
Böleni $0$ a eşitlersek $x=1$ buluruz. Hangi polinomu bölmemiz isteniyorsa o polinomda $x$ yerine $1$ konur. $P(x-1)$ bölünüyor. $x=1$ koyarsak $P(0)$ ı bulmalıyız. Bu bilgiyle ilk kısımda verilen polinoma gidiyoruz.
\begin{align*}
P(x+2)&= x^2-x+7\\
P(0) &= ? \\
\end{align*}
Açıkça görüldüğü gibi $P(0)$ için $x$ yerine $-2$ koymalıyız.
\[ P(-2+2) = (-2)^2-(-2)+7=13 \]
Örnek
$P(x+1) = (m-1)x+3$ ve $P(x)$ polinomu $x-2$ ile tam bölünebiliyorsa $m$ nedir?
Çözüm
Tam bölünüyor demek kalan $0$ demektir. $x-2=0 \rightarrow x=2$. $P(x)$ te $x$ yerine $2$ koyunca kalanı elde etmeliyiz, kalanın değeri de $0$. $P(2)=0$. Bu bilgiyle ilk polinoma gittiğimizde $x$ yerine $1$ koymamız gerektiği anlaşılmaktadır.
\[ P(1+1)=(m-1)\cdot(1) + 3 =0\] Buradan $m= -2 $ çıkar.
$ax^2 +bx+c $ ile bölümünden kalan
Genellikle sorularda hesapların kolaylığı açısından $3x^2-4x+2$ ile bölümünden kalan gibi bir ifade yerine $x^2+x$ veya $x^2+3$ gibi iki terimli ifadeler çıkar. Gene $ax-b$ ile bölerken yaptığımız gibi böleni $0$ a eşitleyeceğiz ancak bu sefer $x^2$ yi çekeceğiz ve $x^2$ yerine bulduğumuz değeri yazacağız. İkinci derece bir ifadeye böldüğümüzde kalan birinci derece olabileceğinden kalanı artık bir sayı olarak değil $ax+b$ olarak alacağız.
Örnek
$P(x)=2x^2-3x-1$ polinomunun $x^2-x$ ile bölümünden kalan nedir?
Çözüm
\[x^2-x=0 \rightarrow x^2 = x\] $x^2$ gördüğümüz yere $x$ yazacağız.
\[ P(x)=2x^2-3x-1 = 2(x)-3x -1 = -x-1 \] Kalan $-x-1$ dir.
$x^2$ yerine eşitini yazdığımızda da karşımıza gene $x^2$ li terimler çıkabilir. Elimizde derecesi $2$ den küçük bir ifade kalana kadar $x^2$ nin eşitini tekrar yazmalıyız. Örneğin:
Örnek
$P(x)=2x^3-x^2+2$ ifadesinin $x^2+x$ ile bölümünden kalan nedir?
Çözüm
\[x^2+x=0 \rightarrow x^2=-x\]
\begin{align*}
P(x) &= 2x^3-x^2+2 =2x^2\cdot x - x^2 +2\\
&=2(-x)\cdot x -(-x) +2 =-2x^2+x+2\\
&=-2(-x)+x+2=3x+2\\
\end{align*}
Kalan $3x+2$ dir.
İki Önemli Soru Tipi
Burada iki önemli ve tipik soruya geçebiliriz. Önce basit olandan başlayalım.
* Bir polinomun ikinci derece bir ifadeye bölümünden kalan verilerek bu ifadenin(bölenin) çarpanlarından birine bölümünden kalan sorulabilir.
Örnekte daha anlaşılır olacaktır.
Örnek
$P(x)$ polinomunun $x^2-1$ ile bölümünden kalan $2x+1$ olduğuna göre $x-1$ ile bölümünden kalan nedir?
Çözüm
$P(x)$ polinomunu $x^2-1$ ile bölersek bölüm bir $Q(x)$ polinomudur ve kalan da (ikinci derece bir ifadeye böldüğümüzden) $ax+b$ şeklindedir. Gene bölmenin tanımından aşağıdaki eşitliği yazabiliriz:
\[ P(x) = (x^2-1) \cdot Q(x) + (2x+1) \]
$x-1$ ile bölümünden kalanı bulmak için $x$ yerine $1$ koymalıyız. $(x-1)$ ifadesi $x^2-1$ in çarpanı olduğundan $x=1$ ikisini de $0$ lamaktadır. Yukarıda yazdığımız ifadede $x$ yerine $1$ koyduğumuzda bu nokta açıkça görülmektedir.
\[ P(x) = (x^2-1) \cdot Q(x) + (2x+1) = 2(1)+1=3\]
Pratik olarak bu sorularda $P(x)$ kalan olarak alınabilir. Örneğin:
Örnek
$P(x)$ polinomunun $x^2+x$ ile bölümünden kalan $-x-3$ olduğuna göre $x$ ile bölümünden kalan nedir?
Çözüm
$P(x)=-x-3$ alabiliriz (İlk örnekte teorik ispatı yapıldı). Böleni $0$ a eşitleyelim ve bu değeri yerine yazalım, $x=0$.
\[ P(0)=0-3=-3 \]
İkinci tip bundan biraz daha zor.
* İki ayrı birinci derece ifadeye bölümünden kalan verilir ve polinomun bunların çarpımına bölümünden kalan sorulur.
Örnek
$P(x)$ polinomunun $(x-2)$ ile bölümünden kalan $1$ ve $(x+1)$ ile bölümünden kalan $-2$ olduğuna göre bu polinomun $x^2-x-2$ ile bölümünden kalan nedir?
Çözüm
Burada $(x-2)$ ve $(x+1)$ in $x^2-x-2$ nin çarpanları olduğuna dikkat edelim. Öncelikle $(x-2)$ ile bölümünden kalan için $x$ yerine $2$ konmalı, $P(2)=1$ ve aynı şekilde $P(-1)=-2$ verilmiş. Bir $P(x)$ polinomunu $x^2-x-2$ ye bölersek bir bölüm çıkar($Q(x)$) ve ikinci derece bir ifadeye böldüğümüzden $ax+b$ şeklinde bir kalan çıkar:
\[ P(x)= (x^2-x-2)\cdot Q(x) + ax+b \] Elimizdeki iki bilgiyi kullanırsak:
\begin{align*}
P(x) &= (x^2-x-2)\cdot Q(x) + ax+b \\
P(2) &= 2a + b=1\\
P(-1) &= -a+b = -2 \\
\end{align*}
Bu soru tipinde de polinom direk $ax+b$ şeklinde düşünülebilir. Çünkü nasılsa verilen bilgiler böleni ($x^2-x-2$) $0$ yapmaktadırlar. İki bilinmeyenimiz ve iki denklemimiz var:
\begin{align*}
2a + b&=1\\
-a+b &= -2 \\
\end{align*}
Bu iki denklemin ortak çözümünden $a=1$ ve $b=-1$ çıkar, kalan $ax+b=x-1$ dir.
Bazen verilene bölmeyebiliriz!
Örnek
$P(x)=2x^{18}-6x^{17}+5x^5-3x+4$ polinomunun $x^2-x+1$ ile bölümünden kalan nedir?
Çözüm
Bir polinomun ikinci derece bir ifadeye bölümünden kalan için kareli terim çekilir ve polinomda yerine yazılır. $x^2-x+1=0$ ve $x^2=x-1$ yapmalıyız. Ancak burada bu mümkün değil. Çünkü polinomun derecesi çok büyük ve birinci dereceye indirgemek çok zor olacak. Bunun yerine $x^2-x+1$ e bölünen bir şeye bölebiliriz.
Örneğin anlaşılması için bir an polinomları bırakalım ve bölünebilmeye geçelim. Bir sayının $5$ e bölümünden kalan sorulsun ve hiç bir kural bilmediğimizi düşünelim. Bu sayıyı $5$ e bölmektense önce $100$ e bölebiliriz. Çünkü $100$ e bölünen kısım zaten $5$ e bölünür, kalanı $5$ e bölmemiz yeterlidir. Örneğin $1249$ sayısının kalanı sorulursa
\[ 1249=12\cdot 100 + 49\] olduğundan ve $12\cdot 100$ lük kısım zaten $5$ e bölüneceğinden sadece $49$ u bölmemiz yeterlidir.
$x^2-x+1$ ifadesi çarpanlara ayırmadan iyi bildiğimiz $x^3+1$ in bir çarpanıdır. [note]$x^3+1=(x+1)(x^2-x+1)$[/note] Polinomu önce $x^3+1$ e böleceğiz. Yani $x^3$ yerine $-1$ yazacağız.
\begin{align*}
P(x)=2x^{18}-6x^{17}+5x^5-3x+4 &=2(x^3)^6-6 (x^3)^5 x^2+5(x^3)x^2-3x+4\\
&=2+6x^2-5x^2-3x+4\\
&=x^2-3x+6
\end{align*}
Elde ettiğimiz kalan $x^2-3x+6$ da $x^2=x-1$ yaparsak kalan $-2x+5$ olur.
Tekrarlarsak $P(x)$ i $x^3+1$ e böldüğümüzde bölüm $Q(x)$ kalan da $x^2-3x+6 $ ise
\[ P(x)= (x^3+1)Q(x)+x^2-3x+6 \]
$(x^3+1)Q(x)$ lik kısım $x^2-x+1$ e tam bölünür.