Ters Fonksiyon Tanımı
Bir fonksiyonun tersi, fonksiyonun yaptığı tüm eşlemeleri ters çevirir. Örneğin $f(3)=5$ ise fonksiyon $3$ ü $5$ e eşliyordur. Bu durumda tersinin de $5$ i $3$ e eşlemesi gerekir. Eski değer kümesi şimdi tanım ve tanım kümesi de değer kümesi olur. Fonksiyonun tersi $f^{-1}$ sembolü ile gösterilir.
\[ f:A\rightarrow B \text{ ise } f^{-1}:B \rightarrow A \]
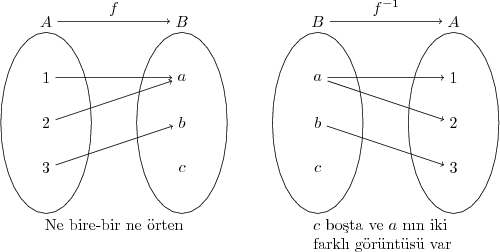
$f^{-1}$ in fonksiyon olabilmesi için $f$ in birebir-örten olması gerekir. Örten olmazsa görüntü kümesinde boşta eleman kalacaktır. Görüntü kümesi ters fonksiyonun tanım kümesi olacağından fonksiyon olmanın birinci şartı çiğnenmiş olur. Bire-bir olmazsa ters çevir-
diğimizde tanım kümesindeki bir eleman değer kümesinde birden fazla elemana eşleşeceğinden fonksiyon olmanın ikinci şartı da ihlal edilecektir.
Ters Fonksiyon Bulunuşu: Doğrusal, İkinci derece, Köklü, Rasyonel ve Permütasyon
Bir fonksiyonun tersinin alınması için:
- $x$ yalnız bırakılır
- $x$ yerine $f^{-1}(x)$ ve $f(x)$ yerine $x$ yazılır.
* Doğrusal Fonksiyonların Tersi
Örnek
$f(x)=2x+3$ fonksiyonunun tersini bulunuz.
Çözüm
\[f(x) =2x+3 \Rightarrow \frac{f(x)-3}{2}= x \Rightarrow \frac{x-3}{2}= f^{-1}(x)\]
İlk adımda $x$ yalnız bırakıldı. İkinci adımda da $x$ ve $f(x)$ yer değiştirdi ve $f$ yerine $f^{-1}$ yazıldı. Daha iyi anlamak için bir sayı değerine bakalım.
\[f(x)=2x+3\Rightarrow f(3)=2.3+3=9\]
$f$ fonksiyonu $3$'ü $9$'a eşliyor. Fonksiyonun tersinin de $9$'u $3$'e götürmesini bekliyoruz.
\[f^{-1}(x){\frac{x-3}{2}}\Rightarrow f^{-1}(9)=\frac{9-3}{2}\Rightarrow f^{-1}(9)=3\]
* İkinci Derece Fonksiyonların Tersi
$f(x)=ax^2+bx+c$ şeklindeki fonksiyonların tersi alınırken tamkare hale getirme yolu kullanılır. Önce $a$ nın $1$ olduğu durumu düşünelim:
Örnek
$f(x)=x^2-4x+7$ fonksiyonunun tersi nedir?
Çözüm
İlk iki terim $x^2-4x=(x-2)^2-4$ tür.
\begin{align*}
y = x^2-4x+7 &= (x-2)^2-4+7\\
&= (x-2)^2+3 \\
y-3 &=(x-2)^2 \\
\sqrt{y-3} &=(x-2) \\
x &= \sqrt{y-3}+2 \\
f^{-1}(x) &=\sqrt{x-3}+2
\end{align*}
$a$ nın $1$ olmadığı durumu $a$ parantezine alıp hallediyoruz.
Örnek
$f(x)=2x^2-3x+1$ fonksiyonunun tersi nedir?
Çözüm
\begin{align*}
y = 2x^2-3x+1 &= 2(x^2-\frac{3}{2}x +\frac{1}{2})\\
\frac{y}{2} &= x^2-\frac{3}{2}x +\frac{1}{2} \\
&= (x-\frac{3}{4})^2-\frac{9}{16} + \frac{1}{2} \\
\frac{y}{2}+\frac{1}{16} &= (x-\frac{3}{4})^2\\
\sqrt{\frac{y}{2}+\frac{1}{16}} &= x-\frac{3}{4}\\
\sqrt{\frac{y}{2}+\frac{1}{16}}+\frac{3}{4} &= x\\
\end{align*}
\[ f^{-1}(x)= \sqrt{\frac{x}{2}+\frac{1}{16}}+\frac{3}{4} \]
* Köklü Fonksiyonların Tersi
Bu fonksiyonlarda ters alınırken köklü ifade yalnız bırakılıp iki tarafın karesi alınır.
Örnek
$f(x)={\sqrt{x}+2}$ fonksiyonunun tersini alınız.
Çözüm
\begin{align*}f(x)&={\sqrt{x}+2}\\
f(x)-2&=\sqrt{x} &\textit{köklü ifadeyi yalnız bıraktık} \\
(f(x)-2)^2&=(\sqrt{x})^2 & \textit{Her iki tarafın karesi}\\
x&=(f(x)-2)^2 & \textit{x'i yalnız bıraktık}\\
f^{-1}(x) &={(x-2)^2} & \textit{$x$ yerine $f^{-1}(x)$ ve $f(x)$ yerine $x$ koyduk}
\end{align*}
Örnek
$f(x)={\frac{\sqrt{x-2}+5}{2}}$ fonksiyonunun tersini bulunuz
Çözüm
\begin{align*}
2f(x)&= \sqrt{x-2}+5 \\
2f(x)-5 &= \sqrt{x-2}\\
[2f(x)-5 ] ^2 &= x-2\\
[2f(x)-5]^2+2 &= x
\end{align*}
Buradan $f^{-1}(x)=(2x-5)^2+2$ çıkar.
* $\displaystyle\frac{ax+b}{cx+d}$ şeklindeki fonksiyonların tersi
Bu tip fonksiyonlarda $x$'i çekmek çok zor olduğu için şöyle bir formül çıkaracağız:
\begin{align*}
y &=\frac{ax+b}{cx+d} \Rightarrow\\
ycx+yd &= ax+b\\
ycx-ax &= b-yd \\
x(yc-a) &= b-yd \\
x &= \frac{-dy + b}{yc - a} \Rightarrow \\
f^{-1}(x) &= \frac{-dx+b}{cx-a}
\end{align*}
Formül şu:
\[f(x)=\frac{ax+b}{cx+d}\qquad\Rightarrow\qquad f^{-1}(x)=\frac{-dx+b}{cx-a}\]
Paydaki $x$'in katsayısı ile paydadaki sabit sayı hem yer hem de işaret değiştiriyor. Dikkat edeceğimiz bir şey hem pay hem de paydanın $mx+n$ şeklinde yazılmış olması.
Örnek
$f(x)=\displaystyle\frac{3x-8}{x-2}$ fonksiyonunun tersi nedir?
Çözüm
Formülü uygularsak $f^{-1}(x)=\displaystyle\frac{2x-8}{x-3}$
Örnek
$f(x)=\displaystyle\frac{3-2x}{x-2}$ fonksiyonunun tersi nedir?
Çözüm
Payı düzeltmemiz gerektiğine dikkat edelim. Önce
$f(x)=\displaystyle\frac{-2x+3}{x-2}$ şekline getirip sonra formülü uygularsak
\[f^{-1}(x)=\frac{2x+3}{x+2}\]
Örnek
$f(x)=\displaystyle\frac{3}{2x-4}$ fonksiyonunun tersi nedir?
Çözüm
Burada da payı $0.x+3$ kabul edeceğiz.
\[f(x)=\frac{0.x+3}{2x-4}\qquad\Rightarrow\qquad f^{-1}(x)=\frac{4x+3}{2x}\]
Bileşke
Fonksiyonlarda bileşke işlemi bir fonksiyondan çıkan değeri diğer fonksiyonun içine atarak gerçekleşir. Bir fonksiyondan çıkan görüntü diğer fonksiyon için tanım kümesi elemanıdır. Örneğin $ f \circ g(x)$ gösteriminde önce $x$ in ilk fonksiyon $g$ de görüntüsü bulunur ve bu $g(x)$ tir. Çıkan görüntünün $f$ de görüntüsü bulunur ve bu da $f(g(x))$ tir. $f$ bileşke $g$ şuna eşittir
\[ f \circ g (x) = f(g(x)) \]
Örneğin $f(x) = 3x+2$ ve $g(x) = x-1$ ise $f \circ g(-1)$ i bulmaya çalışalım
\[ f \circ g(-1) = f(g(-1)) \]
Önce $g(-1)$ i bulacağız ve bulduğumuz değeri $f$ ye koyacağız.
$ g(-1) = -2 $ ve $f(g(-1)) = f(-2) = -4$
Örnekten de anlaşılacağı gibi bileşkede işler sağdan sola doğru işliyor. $f \circ g $ de önce $g(x)$ bulunuyor daha sonra bulunan değeri $f$ alıp görüntüsünü buluyor.
Bileşke fonksiyonun ifadesi için de sağdaki fonksiyon solda $x$ yerine konur. Örneğin yukarıda verilen fonksiyonlar için
\[ f \circ g(x) = (3x+2) \circ (x-1) = 3(x-1) + 2 = 3x-1 \]
Örnek
$ f(x) = 3x + 5$ ve $g(x) = 2x - 8$ ise
- $f \circ g (2)$
- $f \circ f (-1)$
- $g \circ g (1)$
- $ g \circ f(0)$
Çözüm
\begin{align}
f \circ g(2) &= f(g(2)) \\
g(2) &= 2 \cdot 2 - 8 = -4 \\
f(g(2)) &= f(-4) = 3 \cdot -4 + 5 = -7
\end{align}
\begin{align}
f \circ f(-1) &= f(f(-1)) \\
f(-1) &= 3 \cdot (-1) + 5 = 2 \\
f(f(-1)) &= f(2) = 3 \cdot 2 + 5 = 11
\end{align}
\begin{align}
g \circ g(1) &= g(g(1)) \\
g(1) &= 2 \cdot (1) - 8 = -6 \\
g(g(1)) &= g(-6) = 2 \cdot -6 - 8 = -20
\end{align}
\begin{align}
g \circ f(0) &= g(f(0)) \\
f(0) &= 3 \cdot (0) + 5 = 5 \\
g(f(0)) &= g(5) = 2 \cdot 5 - 8 = 2
\end{align}
Bileşkenin özellikleri
- birleşme özelliği: $(f \circ g) \circ h = f \circ (g \circ h)$
- $f \circ f^{-1} = f^{-1} \circ f = I$
- $(f \circ g)^{-1} = g^{-1} \circ f^{-1}$
- değişme özelliği yoktur: $f \circ g =? g \circ f $
