Yarım açı formülleri aslında bir açı ile onun iki katının trigonometrik oranları arası ilişkiyi gösterir. Bu formüller toplam fark formüllerinin doğrudan sonucudur, ancak soru tipi olarak toplam fark formülleri ile ilgili sorulara değil, temel özdeşlik ve sadeleştirme sorularına benzerler. İspatları toplam fark formülleri bölümünde yapıyoruz.
\begin{align*}
\sin (2\theta) &=2 \sin \theta \cos\theta\\%
\cos (2\theta) &= \cos^2 \theta - \sin^2 \theta\\%
&= 2\cos^2 \theta-1 \\ %
&= 1-2\sin^2 \theta\\%
\end{align*}
$\cos (2\theta)$ nın üç formunun da bilinmesi gerekiyor, ancak ilk başta sadece ilk formu bilip $\cos^2$ yerine $1-\sin^2$ ya da $\sin^2$ yerine $1-\cos^2$ yazarak diğer formlara ulaşabiliriz.
Örnek
$\cos x - \sin x = \frac{1}{3}$ ise $\sin 2x$ nedir?
Çözüm
\begin{align*}
(\cos x - \sin x)^2 &= \frac{1}{9}\\
\cos^2 x - 2\sin x \cos x + \sin^2 x &=\frac{1}{9}\\
-2\sin x \cos x &= \frac{1}{9} -1 =\frac{-8}{9} \\
\end{align*}
\[ \sin 2x = \frac{4}{9}\]
Örnek
$\cos^4 \frac{\pi}{12} - \sin^4 \frac{\pi}{12}$ ifadesinin değeri nedir?
Çözüm
\begin{align*}
\cos^4 x - \sin^4 x &= (\cos^2 x-\sin^2 x)(\cos^2 x+\sin^2 x)\\ %
&= \cos^2 x -\sin^2 x \\ %
&= \cos 2x = \cos \frac{\pi}{6} \\%
&= \frac{\sqrt{3}}{2}%
\end{align*}
Örnek
$\sin^4 15^{\circ} + \cos^4 15^{\circ}$ ifadesinin en sade şekli nedir?
Çözüm
\[ a^4+b^4 = (a^2+b^2)^2-2a^2b^2 \]
\begin{align*}
\sin^4 x + \cos^4 x &= (\sin^2 x + \cos^2 x)^2 - 2\sin^2 x \cos^2 x \\
&=1-2 (\sin x \cos x)^2\\
&=1-2(\frac{\sin 2x}{2})^2\\
&= 1 - \frac{\sin^2 2x}{2}
\end{align*}
$x=15^{\circ}$ olduğundan son ifade
\[ 1 - \frac{\sin^2 30^{\circ}}{2} = 1- \frac{1}{8}=\frac{7}{8} \]
Örnek
$\cos 4^{\circ} = x$ ise $\sin 82^{\circ}$ nin $x$ cinsinden değeri nedir?
Çözüm
Bu sorularda açılar arasında bağlantı bulmaya çalışacağız. Önemli olan hangi trigonometrik oranın verilip sorulduğu değil, bu açıları nasıl bağlayacağımız. $82$ yi $90$ a tamamlayan açı $8$ aynı zamanda $4$ ün iki katı.
$ \sin 82 = \cos 8$ olduğundan sadece $\cos 2x$ formülü yeterli.
\begin{align*}
\cos 2x &= 2\cos^2 x -1\\
\cos 8^{\circ} &= 2\cos^2 4^{\circ} -1 = 2x^2 -1 \\
\sin 82^{\circ} &= 2x^2-1
\end{align*}
Örnek
$\cos 4^{\circ} = \sqrt{x}$ ise $\tan 262^{\circ}$ nin $x$ cinsinden değeri nedir?
Çözüm
Gene hangi trigonometrik oran soruluyor, bunun önemi yok. Önce $4$ ve $262$ yi bağlamalıyız. $262=270-8$ olduğundan $8$ in bir oranını bulursak soru çözülmüş oluyor.
\begin{align*}
\cos 2x &= 2\cos^2x-1 \\
\cos 8^{\circ} &= 2 \cos^2 4^{\circ} -1 \\
&= 2x-1
\end{align*}
$\tan 262^{\circ}=\cot 8^{\circ}$ olduğundan bir dik üçgen çizip $\cos 8^{\circ} = 2x-1$ yapmalıyız.
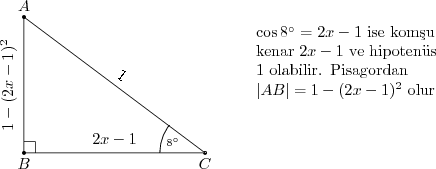
$\cot 8$ değeri $\displaystyle\frac{2x-1}{1-(2x-1)^2}$ olur.
Örnek
$\cos 65 = x$ ise $\sin 40$ ın $x$ cinsinden değeri nedir?
Çözüm
$65$ ten $130$ a yarım açı formülleri ile geçebiliriz. $130$ la $50$ birbirini $180$ e tamamlıyor. $50$ de $40$ ı $90$ a tamamlıyor.
Önce $130$ un bir oranını bulalım.
\[ \cos 130 = 2 \cos^2 65-1 = 2x^2-1\]
\[ \cos 130^{\circ}=-\cos 50^{\circ} = -\sin 40^{\circ}\]
Dolayısıyla cevap $1-2x^2$ dir.
Önemli bir soru:
Örnek
$\frac{\pi}{2} \lt x \lt \pi$ olmak üzere \[ \sqrt{ 2\cos 2x + 2 } \] ifadesinin en sade şekli nedir?
Çözüm
Kök içindeki ifadeyi dışarı çıkarabilmek için $\cos 2x = 2\cos^2x-1$ i kullanmalıyız.
\[ \sqrt{ 2\cos 2x + 2 } = \sqrt{ 2(2\cos^2x-1) + 2 } = \sqrt{ 4\cos^2x-2 + 2}=|2\cos x| \]
Son mutlak değer önemli, $\sqrt{a^2}=|a|$ dır. Eğer $a \lt 0$ ise $-a$ olarak açılacak. Verilen aralıkta kosinüs negatif olduğundan cevap: $-2\cos x$ tir.
Örnek
$0 \lt x \lt \frac{\pi}{4}$ ise $\sqrt{1-\cos 2x}$ ifadesinin eşiti nedir?
Çözüm
Kökten kurtulabilmek için $\cos 2x=1-2\sin^2 x$ i kullanmalıyız.
\[ \sqrt{1-\cos 2x}=\sqrt{1-(1-2\sin^2x)}=\sqrt{2\sin^2x}= \sqrt{2}|\sin x|\]
Verilen aralıkta $\sin x$ pozitiftir. Cevap: $\sqrt{2}\sin x$
Çok önemli bir soru:
Örnek
$0 \lt x \lt \frac{\pi}{4}$ ise $\sqrt{1-\sin 2x}$ ifadesinin en sade şekli nedir?
Çözüm
Kök içindeki ifade bir tam karedir. $1$ yerine $\sin^2 x + \cos^2 x$ ve $\sin 2x =2\sin x \cos x$ yaparsak bu ifade $(a-b)^2$ biçimine getirilmiş olur.
\begin{align*}
\sqrt{1-\sin 2x} &= \sqrt{\sin^2 x + \cos^2 x - 2\sin x \cos x}\\
&= \sqrt{(\sin x - \cos x)^2}\\
&= |\sin x - \cos x|
\end{align*}
$0 \lt x \lt \frac{\pi}{4}$ aralığında kosinüs değeri sinüsten büyüktür. Bu durumda mutlak değerin içi negatiftir.
$|\sin x - \cos x|= \cos x - \sin x$
Örnek
$ \displaystyle\frac{1-\cos 2x}{1+\cos 2x}$ ifadesinin en sade şekli nedir?
Çözüm
$1$ den kurtulabilmek için yukarıda $\cos 2x=1-2\sin^2x$ ve aşağıda da $2\cos^2x-1$ i kullanmalıyız.
\[ \frac{1-\cos 2x}{1+\cos 2x} = \frac{1-(1-2\sin^2x)}{1+(2\cos^2x-1)}=\tan^2x\]
Örnek
\[ \frac{1+\cos x +\cos 2x}{\sin x + \sin 2x} \] ifadesinin en sade şekli nedir?
Çözüm
Paydada $\sin 2x=2\sin x \cos x$ yaptığımızda, $\sin x $ ortak parantezi görünüyor.
\[ \sin x + \sin 2x = \sin x + 2 \sin x \cos x = \sin x (1+2\cos x) \]
Yukarıda da bu çarpanlardan biri çıkmalı ki ifade sadeleşsin. $\cos 2x=2\cos^2 x -1$ dönüşümü yaparsak:
\[ 1+\cos x +\cos 2x = 1 + \cos x + 2\cos^2x-1 =\cos x(2\cos x+1)\]
Dolayısıyla ifadenin en sade şekli: $\cot x $ olmaktadır.
Örnek
$ \frac{1}{\sin 75} + \frac{1}{\cos 75} $ ifadesinin değeri nedir?
Çözüm
$\sin x \cos x = \frac{\sin 2x}{2} $ olduğunu hatırlarsak:
\begin{align*}
\frac{1}{\sin 75} + \frac{1}{\cos 75} &= \frac{\cos 75 + \sin 75}{\sin 75 \cos 75}\\
&= \frac{\cos 75 + \sin 75}{\frac{1}{2}\sin 150}
\end{align*}
$\sin 150 =\sin 30$ olduğundan paydayı hallettik. Ancak $\sin 75+ \cos 75$ ifadesinin cevabını yarım açı formüllerinden nasıl bulacağız?
$\sin 75 + \cos 75 = c$ olsun ve iki tarafın karesini alalım:
\begin{align*}
\sin 75 + \cos 75 &= c\\
(\sin 75 + \cos 75)^2 &= \sin^2 75 + 2\sin 75 \cos 75 + \cos^2 75 =c^2\\
1+2\sin 75\cos 75 &= c^2 \\
1+\sin 150 &= c^2\\
\frac{3}{2}=c^2
\end{align*}
$c^2 = \frac{3}{2}$ olduğundan $c=\pm \frac{\sqrt{3}}{\sqrt{2}}$ dir ve işarete biz karar vermeliyiz. Burada $\sin 75 + \cos 75$ ifadesi kesinlikle pozitiftir.[note1] örneğin $\sin 175+ \cos 175$ olsaydı, kosinüs negatif olduğundan ve açı 135 den büyük olduğundan cevap negatif olacaktı.[/note]
Soru şuna dönüştü:
\[ \frac{\sqrt{\frac{3}{2}}}{\frac{1}{2}\sin 150}= 4\sqrt{\frac{3}{2}} =2\sqrt{6}\]
Örnek
$\sin 100 = x$ ise
\[ \cos 10 \cdot \cos 20 \cdot \cos 40 \cdot \cos 80\] ifadesinin değeri $x$ cinsinden nedir?
Çözüm
Burada açıların birbirinin iki katı olması dikkat çekiyor. $\cos 10$ un yanında bir $\sin 10$ çarpanı olsa $\sin 20$ oluşacak, $\cos 20$ çarpanı bulunduğundan bunlardan $\sin 40$ oluşacak ve böyle devam edecek. İfadeyi $\sin 10$ a çarpıp bölelim:
\begin{align*}
\cos 10 \cdot \cos 20 \cdot \cos 40 \cdot \cos 80 &= \frac{\sin 10 \cos 10 \cdot \cos 20 \cdot \cos 40 \cdot \cos 80}{\sin 10}\\
&= \frac{\frac{\sin 20}{2} \cdot \cos 20 \cdot \cos 40 \cdot \cos 80}{\sin 10}\\
&= \frac{\frac{\sin 40}{4} \cos 40 \cdot \cos 80}{\sin 10}\\
&= \frac{\frac{\sin 80}{8} \cos 80 }{\sin 10}\\
&= \frac{\sin 160}{16\sin 10}
\end{align*}
Bize verilen $\sin 100 = \cos 10$ ve payda $\sin 160$ bulduk. $\sin 160=\sin 20 = 2 \sin 10 \cos 10$
\[ \frac{\sin 160}{16\sin 10}=\frac{2 \sin 10 \cos 10}{16\sin 10}=\frac{\cos 10}{8} =\frac{x}{8}\]
