Bir karmaşık sayının köklerini hem kutupsal biçimde hem de $a+ib$ biçiminde iken öğreneceğiz. Önce kutupsal biçimle başlayalım.
Kutupsal Biçimde Kökler
\[ z=r \text{ cis } \theta \] şeklinde verilen bir karmaşık sayının $n.$ dereceden kökleri $n$ tanedir ($w_0, w_1 \cdots w_{n-1}$ olsunlar) ve aşağıdaki formülle bulunurlar:
\[ w_k = \sqrt[n]{r} \text{ cis } (\frac{ \theta + 2k\pi}{n}) \qquad k = 0,1,2 \cdots n-1 \]
Formül karışık görünse de aşağıdaki çözümlü örneklerde aslında kökleri bulmanın basitliği görülecektir. Formülü sözel anlatırsak bir karmaşık sayının $n.$ dereceden köklerini($n$ tanedirler) bulmak için modülün $n.$ dereceden kökü alınır. İlk kökün argümanı için verilen karmaşık sayının argümanı, kök derecesi $n$ e bölünür. Bundan sonraki köklerin argümanları için de $\frac{2\pi}{n}$ ekleriz. Örneğin:
Örnek
$ z = 4\text{ cis }30^{\circ} $ sayısının karekökleri nelerdir?
Çözüm
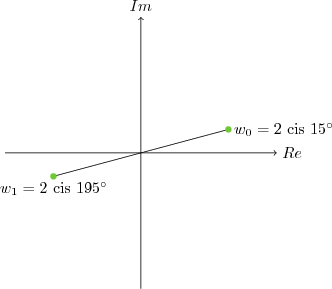
Kökler iki tanedir: $w_0$ ve $w_1$. Köklerin modülleri için $z$ nin modülünün karekökü alınır ve ilk kökün argümanı da $z$ nin argümanı $2$ ye bölünerek bulunur (kök derecesi $2$). Yani ilk kök \[ w_0 = 2 \text{ cis }15^{\circ} \]
Bundan sonraki kök için $360^{\circ}$ kök derecesine bölünür: $360:2=180$ ve bu değer ilk kökün argümanına eklenir.
\[ w_1= 2 \text{ cis }195^{\circ} \]
* Karekökler birbirinden $\pi$ ya da $180^{\circ}$ uzaklıktadır.
Örnek
$ z = 8 \text{ cis }60^{\circ} $ sayısının küpkökleri nelerdir?
Çözüm
Kökler üç tanedir: $w_0, w_1,$ ve $w_2$. İlk kök için $z$ nin modülünün küpkökü alınır. İlk kökün argümanı için de $z$ nin argümanı kök derecesine bölünür.
\[ w_0 = 2 \text{ cis }20^{\circ} \] Bundan sonraki kökler için $360$ kök derecesine bölünür, $360:3=120$. Bulunan değer ilk kökün argümanına eklenerek ikinci kök, buna da eklenerek üçüncü kök bulunur.
\[ w_1 = 2 \text{ cis }(20+120)^{\circ} = 2 \text{ cis }(140)^{\circ} \]
\[ w_2 = 2 \text{ cis }(140+120)^{\circ} = 2 \text{ cis }(260)^{\circ} \]
* Küpkökler birbirinden $\frac{2\pi}{3}$ ya da $120^{\circ}$ uzaklıktadır.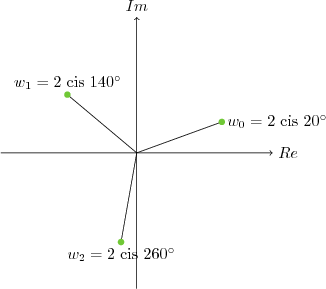
Kutupsal biçimde kökler formülü ispatı
İspatı karekök ve küp kök için yapacağız.
Bir $z=r \text{ cis }\theta$ karmaşık sayısı verilmiş olsun. Bu sayının varsa kareköküne $w=r_w \text{ cis } \alpha$ diyelim. Bu sayı $z$ nin karekökü olduğundan karesi $z$ ye eşit olmalıdır:
\begin{align*}
w^2 &= z \\
(r_w \text{ cis } \alpha)^2 &= r \text{ cis } \theta \\
r_w^2 \text{ cis } (2 \alpha) &= r \text{ cis } \theta \\
r_w^2 = r & \text{ ve } \text{ cis } 2\alpha = \text{ cis } \theta\\
\end{align*}
$(r_w \text{ cis } \alpha)^2=r_w^2 \text{ cis } (2 \alpha) $ yazarken kutupsal biçimde üs almada yazdığımız kuralı kullandık. Son eşitliklerden birincisinden $r_w= \pm \sqrt{r}$ çıkar ancak modül her zaman pozitif olduğundan $r_w= \sqrt{r}$ dır.
İkinci eşitlik trigonometrik bir denklem ve $\text{ cis }$ kosinüs ve sinüs değerlerini içerdiğinden bu iki açının $\cos$ ve $\sin$ değerleri aynı olmalıdır. Bu durumda ya iki açı aynıdır ya da biri diğerine $360^{\circ}$ ekleyip çıkarılarak bulunabilir (esas ölçülerinin aynı olması yeterlidir).
\begin{align*}
2 \alpha &= \theta + 2k\pi \\
\alpha &= \frac{ \theta + 2k\pi}{2} \\
\end{align*}
Burada $k=0$ ve $k=1$ iki ayrı açı üretir.
\[ w_0 = \sqrt{r} \text{ cis } \frac{\theta}{2} \qquad w_1= \sqrt{r} \text{ cis } \frac{\theta+2\pi}{2} \]
$k=2$ koymak anlamsızdır bu durumda açı $\theta + 2\pi$ olacağından bulacağımız sayı $w_0$ a eşit olur, dolayısıyla iki farklı kök vardır.
Benzer şekilde $z$ nin küpkökleri için de elimizde şu eşitlik vardır:
\begin{align*}
w^3 &= z \\
(r_w \text{ cis } \alpha)^3 &= r \text{ cis } \theta \\
r_w^3 \text{ cis } (3 \alpha) &= r \text{ cis } \theta \\
r_w^3 = r & \text{ ve }\text{ cis } 3\alpha = \text{ cis } \theta\\
\end{align*}
Buradan $r_w= \sqrt[3]{r}$ ve şu trigonometrik denklem çıkar:
\begin{align*}
3 \alpha &= \theta + 2k\pi \\
\alpha &= \frac{ \theta + 2k\pi}{3} \\
\end{align*}
$k=0,1$ ve $2$ farklı sayılar üretir bundan sonraki değerler gene aynı sayılara döner.
\[ w_0 = \sqrt[3]{r} \text{ cis } \frac{\theta}{3} \qquad w_1= \sqrt[3]{r} \text{ cis } \frac{\theta+2\pi}{3} \qquad w_2= \sqrt[3]{r} \text{ cis } \frac{\theta+4\pi}{3} \]
Kartezyen Biçimde Karekök Bulunuşu
$z=a+ib$ şeklinde verilen bir sayının karekökleri için aşağıda çıkarılan üç eşitlik kullanılabilir:
Verilen karmaşık sayının karekökü $w = x+iy$ olsun, bu durumda
\begin{align*}
w^2 &= z\\
(x+iy)^2 &= a+ib\\
x^2-y^2 + 2xyi &= a+ib
\end{align*}
Buradan iki eşitlik çıkmaktadır:
\begin{align*}
x^2-y^2 &= a \\
2xy &= b
\end{align*}
Bunların yanında üçüncü eşitliği bulmak için modülden gelen aşağıdaki eşitliği kullanacağız:
\begin{align*} |w^2| &= |z|\\ |w|^2 &= |z| \\ x^2 + y^2 &= \sqrt{a^2 + b^2}\\
\end{align*}
Toparlarsak kullanacağımız üç eşitlik:
\begin{align*}
x^2-y^2 &= a \\
2xy &= b \\
x^2 + y^2 &= |z|\\
\end{align*}
Örnek
$z=5-12i$ sayısının kareköklerini bulunuz.Çözüm
Üç eşitliği yazarsak:
\begin{align*}
x^2-y^2 &= a & x^2-y^2 &= 5 \\
2xy &= b & 2xy &= -12 \\
x^2 + y^2 &= |z| & x^2+y^2 &= 13
\end{align*}
Birinci ve üçüncü denklemleri alt alta toplarsak $x^2 = 9$ ve $x=\pm 3$ olur. Birinci veya üçüncü denklemden $x^2=9$ ise $y^2=4$ ve $y=\pm 2$ çıkar. $x=3$ için $y=-2$ ve $x=-3$ için de $y=2$ olması gerektiği de ikinci denklemden çıkmaktadır. Çözüm $(3,-2)$ ve $(-3,2)$ ikilileridir ya da \[ w_0 = 3-2i \qquad w_1= -3+2i\] olur.
Örnek
$z=3 + 4i$ sayısının kareköklerini bulunuz.Çözüm
Üç eşitliği yazarsak:
\begin{align*}
x^2-y^2 &= a & x^2-y^2 &= 3 \\
2xy &= b & 2xy &= 4 \\
x^2 + y^2 &= |z| & x^2+y^2 &= 5
\end{align*}
Birinci ve üçüncü denklemleri alt alta toplarsak $x^2 = 4$ ve $x=\pm 2$ olur. Birinci veya üçüncü denklemden $x^2=4$ ise $y^2=1$ ve $y=\pm 1$ çıkar. $x=2$ için $y=1$ ve $x=-2$ için de $y=-1$ olması gerektiği de ikinci denklemden çıkmaktadır. Çözüm $(2,1)$ ve $(-2,-1)$ ikilileridir ya da \[ w_0 = 2+i \qquad w_1= -2-i\] olur. Bu örnekte sağlamasını da yapalım. Bulduğumuz sayıların kareleri $3+4i$ ye eşit olmalıdır:
\[ (2+i)^2 = 4 + 4i -1=3+4i \] $-2-i = -(2+i)$ olduğundan karesi $2+i$ ile aynıdır.
